Integrating and plotting an orbit in an NFW potential#
We first need to import some relevant packages:
>>> import astropy.units as u
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import gala.integrate as gi
>>> import gala.dynamics as gd
>>> import gala.potential as gp
>>> from gala.units import galactic
In the examples below, we will work use the galactic
UnitSystem: as I define it, this is: \({\rm kpc}\),
\({\rm Myr}\), \({\rm M}_\odot\).
We first create a potential object to work with. For this example, we’ll use a spherical NFW potential, parametrized by a scale radius and the circular velocity at the scale radius:
>>> pot = gp.NFWPotential.from_circular_velocity(v_c=200*u.km/u.s,
... r_s=10.*u.kpc,
... units=galactic)
As a demonstration, we’re going to first integrate a single orbit in this potential.
The easiest way to do this is to use the
integrate_orbit method of the potential object,
which accepts a set of initial conditions and a specification for the
time-stepping. We’ll define the initial conditions as a
PhaseSpacePosition object:
>>> ics = gd.PhaseSpacePosition(pos=[10,0,0.] * u.kpc,
... vel=[0,175,0] * u.km/u.s)
>>> orbit = gp.Hamiltonian(pot).integrate_orbit(ics, dt=2., n_steps=2000)
This method returns a Orbit object that contains an
array of times and the (6D) position at each time-step. By default, this method
uses Leapfrog integration to compute the orbit
(LeapfrogIntegrator), but you can optionally specify
a different (more precise) integrator class as a keyword argument:
>>> orbit = gp.Hamiltonian(pot).integrate_orbit(ics, dt=2., n_steps=2000,
... Integrator=gi.DOPRI853Integrator)
We can integrate many orbits in parallel by passing in a 2D array of initial conditions. Here, as an example, we’ll generate some random initial conditions by sampling from a Gaussian around the initial orbit (with a positional scale of 100 pc, and a velocity scale of 1 km/s):
>>> norbits = 128
>>> new_pos = np.random.normal(ics.pos.xyz.to(u.pc).value, 100.,
... size=(norbits,3)).T * u.pc
>>> new_vel = np.random.normal(ics.vel.d_xyz.to(u.km/u.s).value, 1.,
... size=(norbits,3)).T * u.km/u.s
>>> new_ics = gd.PhaseSpacePosition(pos=new_pos, vel=new_vel)
>>> orbits = gp.Hamiltonian(pot).integrate_orbit(new_ics, dt=2., n_steps=2000)
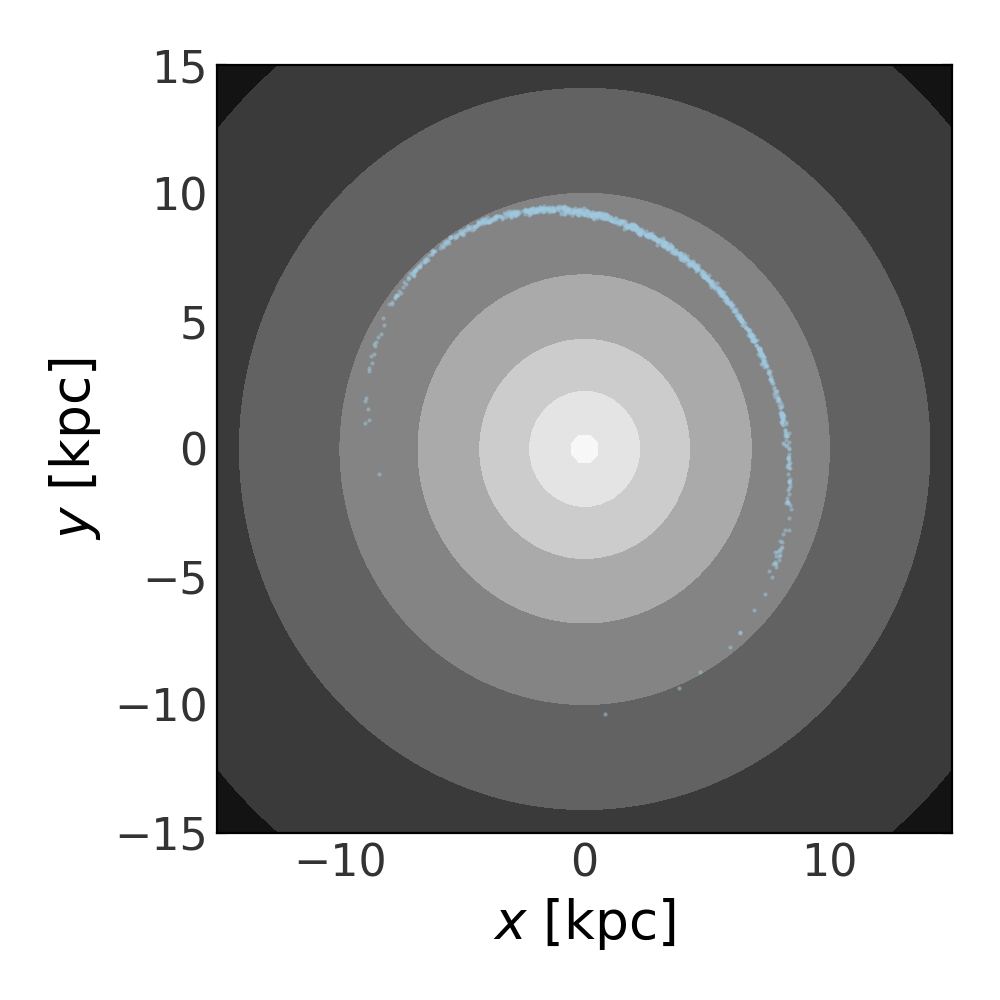
We’ll now plot the final positions of these orbits over isopotential contours.
We use the plot_contours() method of the potential
object to plot the potential contours. This function returns a
Figure object, which we can then use to over-plot
the orbit points:
>>> grid = np.linspace(-15,15,64)
>>> fig,ax = plt.subplots(1, 1, figsize=(5,5))
>>> fig = pot.plot_contours(grid=(grid,grid,0), cmap='Greys', ax=ax)
>>> fig = orbits[-1].plot(['x', 'y'], color='#9ecae1', s=1., alpha=0.5,
... axes=[ax], auto_aspect=False)
(Source code, png, pdf)