Integrating an orbit in a rotating reference frame#
We first need to import some relevant packages:
>>> import astropy.units as u
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import gala.integrate as gi
>>> import gala.dynamics as gd
>>> import gala.potential as gp
>>> from gala.units import galactic
>>> from scipy.optimize import minimize
Orbits in a barred galaxy potential#
In the example below, we will work use the galactic
UnitSystem: as I define it, this is: \({\rm kpc}\),
\({\rm Myr}\), \({\rm M}_\odot\).
For this example, we’ll use a simple, analytic representation of the potential
from a Galactic bar and integrate an orbit in the rotating frame of the bar,
which has some pattern speed \(\Omega\). We’ll use a three-component
potential model consisting of the bar (an implementation of the model used in
Long & Murali 1992), a
Miyamoto-Nagai potential for the galactic disk, and a spherical NFW potential
for the dark matter distribution. We’ll tilt the bar with respect to the x-axis
by 25 degrees (the angle alpha below). First, we’ll define the disk and
halo potential components:
>>> disk = gp.MiyamotoNagaiPotential(m=6E10*u.Msun,
... a=3.5*u.kpc, b=280*u.pc,
... units=galactic)
>>> halo = gp.NFWPotential(m=6E11*u.Msun, r_s=20.*u.kpc, units=galactic)
We’ll set the mass of the bar to be 1/6 the mass of the disk component, and we’ll set the long-axis scale length of the bar to \(4~{\rm kpc}\). We can now define the bar component:
>>> bar = gp.LongMuraliBarPotential(m=1E10*u.Msun, a=4*u.kpc,
... b=0.8*u.kpc, c=0.25*u.kpc,
... alpha=25*u.degree,
... units=galactic)
The full potential is the composition of the three potential objects. We can
combine potential classes by defining a CCompositePotential
class and adding named components:
>>> pot = gp.CCompositePotential()
>>> pot['disk'] = disk
>>> pot['halo'] = halo
>>> pot['bar'] = bar
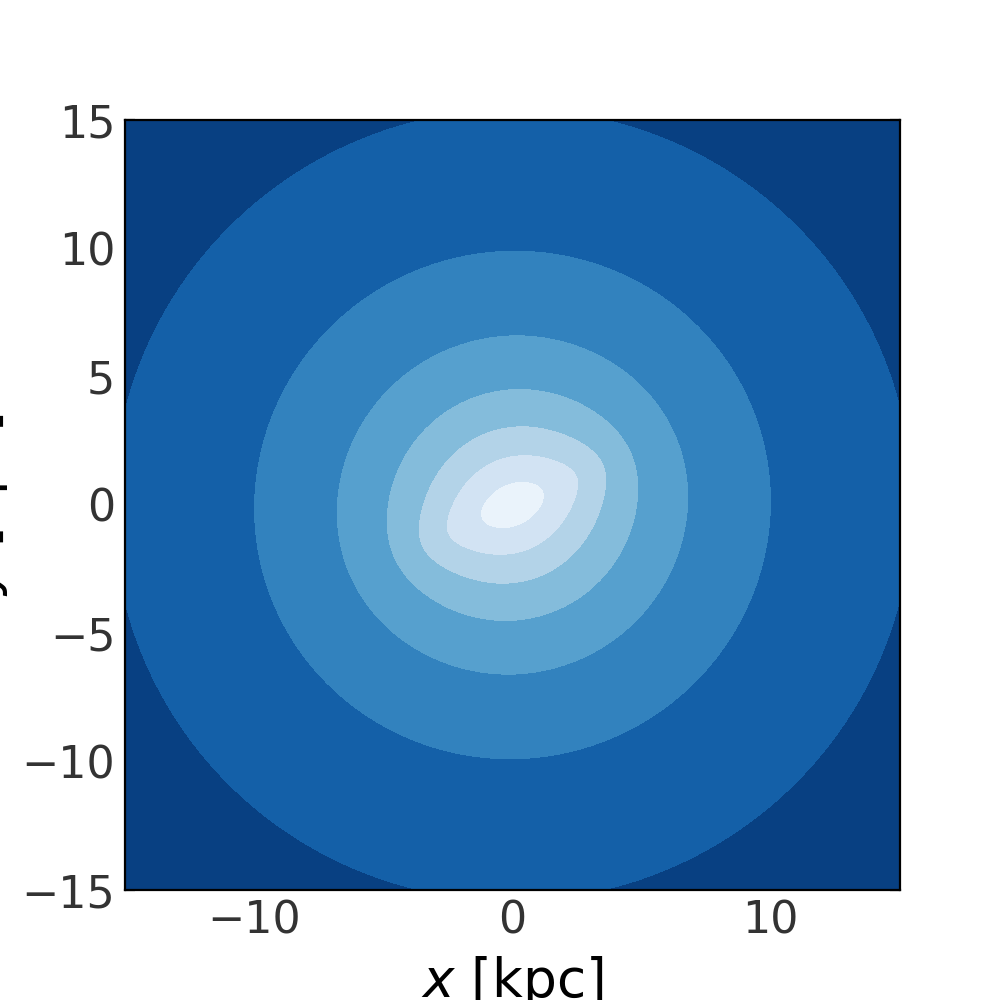
Let’s visualize the isopotential contours of the potential in the x-y plane to see the bar perturbation:
>>> grid = np.linspace(-15,15,128)
>>> fig, ax = plt.subplots(1, 1, figsize=(5,5))
>>> fig = pot.plot_contours(grid=(grid,grid,0.), ax=ax)
>>> ax.set_xlabel("$x$ [kpc]")
>>> ax.set_ylabel("$y$ [kpc]")
(Source code, png, pdf)
We assume that the bar rotates around the z-axis so that the frequency vector is
just \(\boldsymbol{\Omega} = (0,0,42)~{\rm km}~{\rm s}^{-1}~{\rm
kpc}^{-1}\). We’ll create a
Hamiltonian object with a
ConstantRotatingFrame with this
frequency:
>>> Om_bar = 42. * u.km/u.s/u.kpc
>>> frame = gp.ConstantRotatingFrame(Omega=[0,0,Om_bar.value]*Om_bar.unit,
... units=galactic)
>>> H = gp.Hamiltonian(potential=pot, frame=frame)
We can now numerically find the co-rotation radius in this potential and integrate an orbit from a set of initial conditions near the co-rotation radius:
>>> import scipy.optimize as so
>>> def func(r):
... Om = pot.circular_velocity([r[0], 0, 0]*u.kpc)[0] / (r[0]*u.kpc)
... return (Om - Om_bar).to(Om_bar.unit).value**2
>>> res = so.minimize(func, x0=10., method='powell')
>>>
>>> r_corot = res.x[0] * u.kpc
>>> v_circ = Om_bar * r_corot * u.kpc
>>>
>>> w0 = gd.PhaseSpacePosition(pos=[r_corot.value, 0, 0] * r_corot.unit,
... vel=[0, v_circ.value, 0.] * v_circ.unit)
>>> orbit = H.integrate_orbit(w0, dt=0.1, n_steps=40000,
... Integrator=gi.DOPRI853Integrator)
>>> fig = orbit.plot(marker=',', linestyle='none', alpha=0.5)
>>> for ax in fig.axes:
... ax.set_xlim(-15,15)
... ax.set_ylim(-15,15)
(Source code, png, pdf)
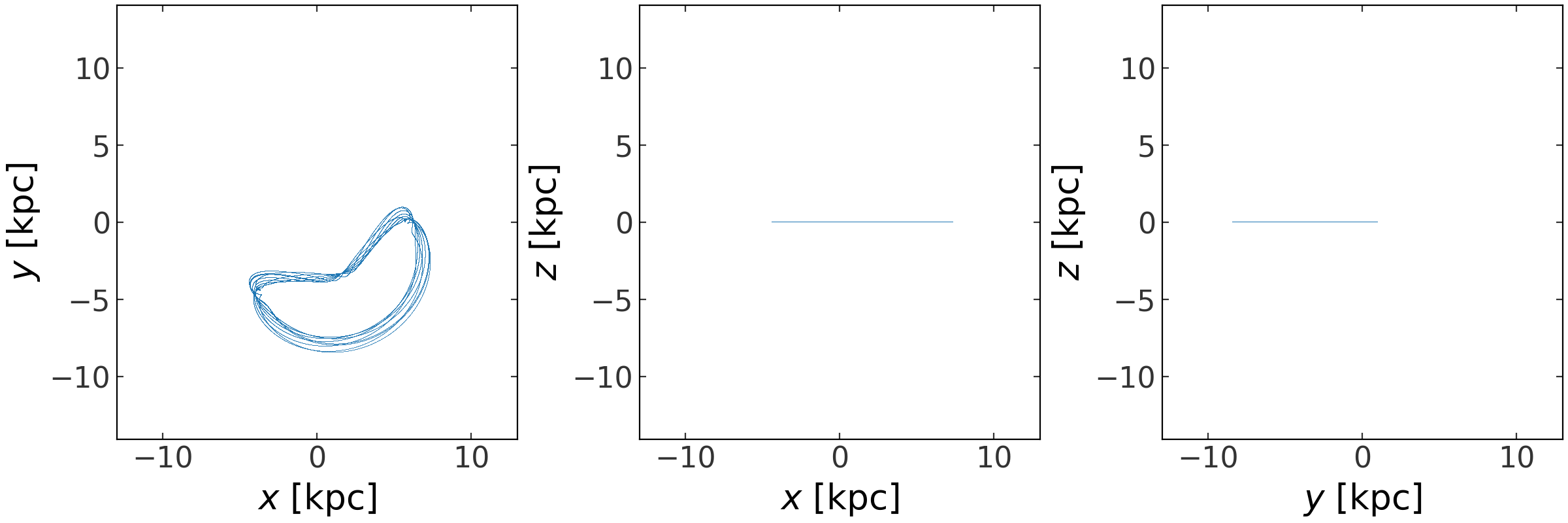
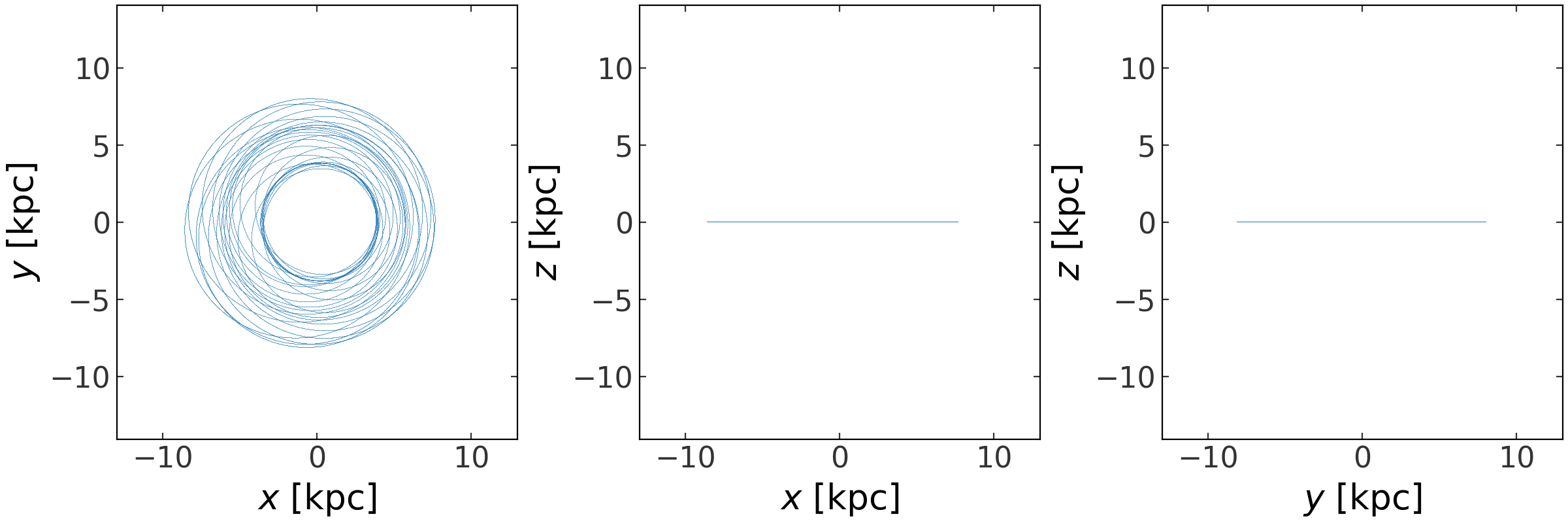
This is an orbit circulation around the Lagrange point L5! Let’s see what this orbit looks like in an inertial frame:
>>> inertial_orbit = orbit.to_frame(gp.StaticFrame(galactic))
>>> fig = inertial_orbit.plot(marker=',', linestyle='none', alpha=0.5)
>>> for ax in fig.axes:
... ax.set_xlim(-15,15)
... ax.set_ylim(-15,15)
(Source code, png, pdf)